1
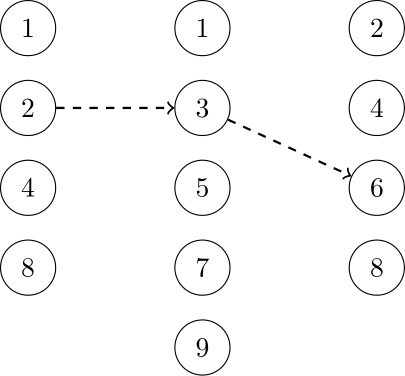
Betty quiere dibujar caminos conectando un número de la primera columna, un número de la segunda columna y un número de la tercera columna. Por ejemplo, puede dibujar un camino que conecte el 2 de la primera columna con el 3 de la segunda columna con el 6 de la tercera columna, como se ve en la figura.

Quiere que en todos los caminos que dibuja, la suma de los tres números del camino sea siempre la misma (puede ser una suma distinta a la del ejemplo).
Si quiere dibujar la mayor cantidad posible de caminos, ¿cuántos caminos puede dibujar? ¿Cuánto suman los números en cada camino? ¿Cuáles son todos los caminos que dibuja?
Ingresar solución de este problema.
2
Mario escribe un número de tres dígitos en cada uno de los tres círculos. Quiere que el segundo número sea el doble del primero, y el tercero el doble del segundo. Además quiere que la suma de los dígitos del primer número sea 7, del segundo 14 y del tercero 19.
¿Qué números puede colocar? Dar todas las posibilidades.

Ingresar solución de este problema.
3
Ana, Beto, Carla, Daniela, Eduardo y Fernanda fueron al teatro y se sentaron en una fila de 6 asientos todos juntos, en algún orden. En el medio de la función todos van al baño. Al volver se sientan en los mismos seis asientos, pero en distinto orden:
¿Cómo estaban sentados originalmente los seis amigos? ¿Cómo se sentaron después de los intercambios? Dar todas las posibilidades.
Ingresar solución de este problema.
Ver soluciones enviadas por tu club hasta el momento.
| Olimpíada Matemática Argentina www.oma.org.ar |
||
| mensajes mateclubes@oma.org.ar |